Queues in an Interactive Random Environment

Collaborators: Hans Daduna, Ruslan Krenzler, Sonja Otten Link to heading

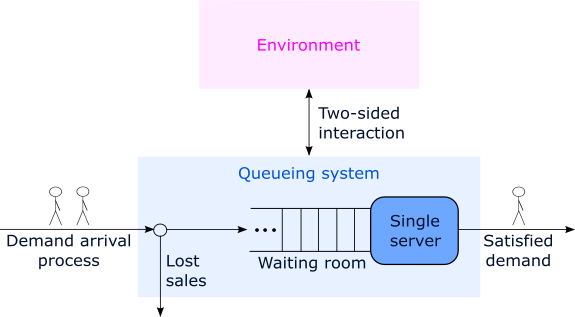
We consider exponential single server queues with state dependent arrival and service rates which evolve under influences of external environments [1,2]. The transitions of the queues are influenced by the environment’s state and the movements of the environment depend on the status of the queues (bi-directional interaction). The environment is constructed in a way to encompass various models from the recent Operations Research literature, where a queue is coupled with an inventory or with reliability issues. With a Markovian joint queueing-environment process we prove separability for a large class of such interactive systems, i.e. the steady state distribution is of product form and explicitly given. The queue and the environment processes decouple asymptotically and in steady state. For non-separable systems we develop ergodicity criteria via Lyapunov functions. By examples we show principles for bounding throughputs of non-separable systems by throughputs of two related separable systems as upper and lower bound.

References Link to heading

[1] S. Otten, R. Krenzler, H. Daduna, and K. Kruse. Exponential single server queues in an interactive random environment. Stochastic Systems, 13(2):271–319, 2023. doi
[2] S. Otten. Integrated Models for Performance Analysis and Optimization of Queueing-Inventory-Systems in Logistic Networks. PhD thesis, Universität Hamburg, 2017. urn